10 дивовижних парадоксів, які поставлять вас в глухий кут. Частина 1

 

Парадокси можна зустріти скрізь, від екології до геометрії й від логіки до хімії. Навіть компʼютер, на якому ви читаєте статтю, сповнений парадоксів. Ось п’ять з  десяти пояснень досить захопливих парадоксів. Деякі з них настільки дивні, що ми просто не можемо до кінця зрозуміти, в чому суть. Сьогодні ми розглянемо 5-ть таких парадоксів

1. Парадокс Банаха-Тарського

Уявіть, що ви тримаєте в руках мʼячик. А тепер уявіть, що ви почали розривати цю кульку на шматки, і шматочки можуть бути будь-якої вподобаної форми. Потім складіть шматочки разом так, щоб вийшло дві кульки замість одної. Який буде розмір цих кульок в порівнянні з оригінальним мʼячем? Відповідно до теорії множин, отримані кульки будуть того ж розміру і форми, що і вихідний куля. Крім того, якщо врахувати, що кульки мають різний обʼєм, то будь-яка з кульок може трансформуватися відповідно до іншої.

Це призводить до висновку, що горох можна розділити на кульки розміром з Сонце. Хитрість парадоксу полягає в тому, що ви можете розривати кулі на шматочки будь-якої форми. На практиці зробити це неможливо - будова матеріалу і, в кінцевому рахунку, розміри атомів накладають деякі обмеження.

Для того щоб дійсно можна було розбити кулю так, як вам більше подобається, вона повинна містити нескінченну кількість доступних нульових точок. Тоді куля з таких точок буде нескінченно щільною, а коли її розірвати, форми шматочків можуть вийти настільки складними, що не матимуть певного обʼєму. І ви можете зібрати ці шматочки, кожна з яких містить нескінченну кількість точок, в нову кульку будь-якого розміру. Нова куля як і раніше буде складатися з нескінченних точок, причому обидві кулі будуть однаково нескінченно щільними.

Якщо спробувати втілити ідею в життя, нічого не вийде. Але все виходить чудово при роботі з математичними сферами - нескінченно подільними числовими множинами в тривимірному просторі. Розвʼязаний парадокс називається теоремою Банаха-Тарського і грає величезну роль в математичній теорії множин.

2. Парадокс Пето

Очевидно, що кити набагато більші за нас, а значить, у них в організмі набагато більше клітин. І кожна клітина в організмі теоретично може стати злоякісною. Тому кити набагато частіше хворіють на рак, ніж люди, чи не так? Не зовсім. Парадокс Пето, названий на честь оксфордського професора Річарда

Пето, стверджує, що немає кореляції між розміром тварин і раком. Люди і кити мають приблизно однакові шанси захворіти на рак, але деякі породи крихітних мишей мають набагато більше шансів. Деякі біологи вважають, що відсутність кореляції в парадоксі Пето можна пояснити тим, що більші тварини краще протистоять пухлин: механізм працює таким чином, щоб запобігти мутації клітин в процесі ділення.

3. Проблема теперішнього часу

Щоб щось фізично існувало, воно повинно бути присутнім в нашому світі деякий час. Не може бути обʼєкта без довжини, ширини і висоти, і не може бути обʼєкта без «тривалості» — «миттєвого» обʼєкта, тобто такого, який не існує хоча б якийсь проміжок часу, не існує взагалі.

Згідно універсальному нігілізму, минуле і майбутнє не займають часу в сьогоденні. Крім того, неможливо кількісно визначити тривалість, яку ми називаємо «теперішнім часом»: будь-яку кількість часу, яке ви назвете «теперішнім часом», можна розділити на частини - минуле, теперішнє і майбутнє.

Якщо сьогодення триває, скажімо, секунду, то цю секунду можна розділити на три частини: перша частина буде минулим, друга - сьогоденням, а третя - майбутнім. Третину другої, яку ми зараз називаємо сьогоденням, також можна розділити на три частини. Напевно ви вже зрозуміли ідею - так можна продовжувати нескінченно.

Таким чином, сьогодення насправді не існує, тому що воно не триває в часі. Універсальний нігілізм використовує цей аргумент, щоб довести, що взагалі нічого немає.

4. Парадокс Моравека

При вирішенні завдань, що вимагають вдумливих міркувань, у людей виникають труднощі. З іншого боку, основні моторні та сенсорні функції, такі як ходьба, взагалі не викликають жодних труднощів. Але коли справа доходить до компʼютерів, все навпаки: компʼютерам дуже легко вирішувати складні логічні завдання, такі як розробка шахової стратегії, але набагато складніше запрограмувати компʼютер так, щоб він міг ходити або відтворювати людську мову. Ця відмінність між природним і штучним інтелектом відома як парадокс Моравека.

Ганс Моравец, науковий співробітник кафедри робототехніки Університету Карнегі-Меллона, пояснює це спостереження ідеєю зворотної інженерії нашого власного мозку. Реверс- інжиніринг найскладніше виконувати на завданнях, які люди виконують несвідомо, таких як рухові функції.

Оскільки абстрактне мислення стало частиною людської поведінки менше 100 000 років тому, наша здатність вирішувати абстрактні проблеми є свідомою. Таким чином, нам набагато легше створити технологію, яка імітує цю поведінку. З іншого боку, ми не розуміємо таких дій, як ходьба або розмова, тому нам складніше змусити штучний інтелект робити те ж саме.

5. Закон Бенфорда

Яка ймовірність того, що випадкове число почнеться з числа «1»? Або з цифрою «3»? Або з "7"? Якщо ви мало знайомі з теорією ймовірностей, ви можете припустити, що ймовірність становить один з дев'яти, або приблизно 11%.

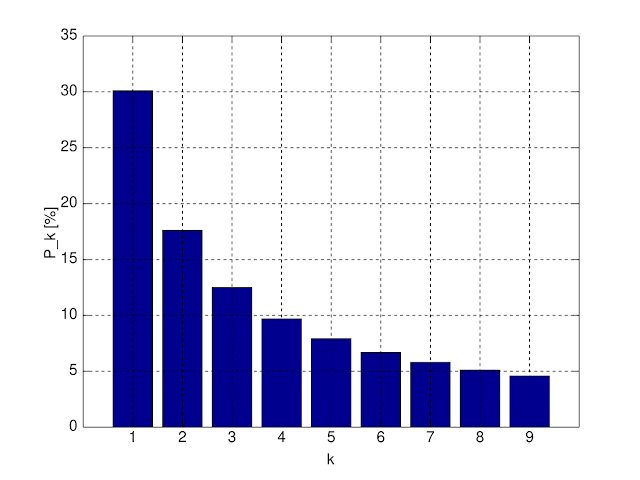
Якщо подивитися на реальні цифри, можна помітити, що «9» зустрічається набагато рідше, ніж в 11% випадків. Крім того, набагато менше цифр, ніж очікувалося, починаються з «8», але колосальні 30% чисел починаються з цифри «1». Ця парадоксальна закономірність проявляється у всіляких реальних випадках, від чисельності населення до цін на акції та довжин річок.

Фізик Френк Бенфорд вперше відзначив це явище в 1938 році. Він встановив, що частота появи цифри як першої падає в міру збільшення цифри від одиниці до девʼяти. Тобто «1» зʼявляється як перша цифра приблизно в 30,1% випадків, «2» зʼявляється приблизно в 17,6% випадків, «3» приблизно в 12,5%, і так до тих пір, поки «9» не з'явиться як перша цифра тільки в 4,6% випадків. Щоб зрозуміти це, уявіть, що ви нумеруєте лотерейні квитки послідовно. Коли у вас пронумеровані квитки від одного до девʼяти, ймовірність того, що будь-яка цифра буде першою, становить 11.1%. Коли ви додаєте квиток номер 10, ймовірність випадкового числа, що починається з «1», збільшується до 18,2%. Ви додаєте квитки з No 11 на No 19, і ймовірність того, що номер квитка починається з «1», продовжує зростати, досягаючи максимуму в 58%. Тепер ви додаєте квиток номер 20 і продовжуєте нумерувати квитки. Шанс того, що число почнеться з «2», зростає, а ймовірність того, що воно почнеться з «1», повільно зменшується.

Закон Бенфорда поширюється не на всі випадки розподілу чисел. Наприклад, набори чисел, діапазон яких обмежений (людський зріст або вага), не підпадають під дію закону. Він також не працює з наборами, які мають лише один або два порядки.

Однак закон застосовується до багатьох типів даних. В результаті влада може використовувати закон для виявлення шахрайства: коли надана інформація не відповідає закону Бенфорда, влада може зробити висновок, що хтось сфабрикував дані.

Ми з вами розглянули 5-ть захоплюючих парадоксів, решту розг

лянемо наступного тижня серед них будуть: “С-парадокс”, “Безсмертна мураха на мотузці”, “Парадокс екологічної рівноваги”, “Парадокс Тритона”, “Ефект Мпемби”. До зустрічі в наступний понеділок.

Климчук Артемія